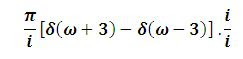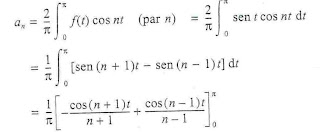Un ejemplo práctico de cómo calcular un espectro es:
Sea la función f(t) = Sen (3t), calcule su espectro.
Como anteriormente lo mencionamos un espectro es el modulo de la transformada de fourier, entonces procedemos a realizar la transformada.
2009-11-10
Espectro de Fourier
Definición:
-El espectro de frecuencia de un fenómeno ondulatorio (sonoro, luminoso o electromagnético), es una medida de la distribución de amplitudes de cada frecuencia.
-Se puede decir que un espectro de Fourier no es más que, el módulo de la transformada de Fourier.
Es decir simplemente tenemos que sacar el módulo de la expresión de la transformada, y para sacar un módulo, simplemente sacamos la raíz de las componentes elevadas al cuadrado.
En el caso de la transformada de fourier se tiene como componentes la parte imaginaria (Img) y la parte real (Re), luego de sacar este módulo procedemos a graficar, pero no siempre va a ser fácil graficar puesto que los módulos de esta transformada pueden salir muy complejos, es por eso que se recomienda la ayuda de un material electrónico como los programas de computadora, uno de los mejores software para realizar funciones es (MatLab).
Datos curiosos en las Matemáticas
1. Cuenta la leyenda que Sessa, inventor del ajedrez, presentó el juego a Sherán, príncipe de la India, quien quedó maravillado de lo ingenioso que era y de la variedad de posiciones que en él eran posibles. Con el fin de recompensarle, le preguntó qué deseaba. Sessa le pidió un corto plazo para meditar la respuesta. Al día siguiente se presentó ante el soberano y le hizo la siguiente petición: «Soberano, manda que me entreguen un grano de trigo por la primera casilla del tablero de ajedrez, dos granos por la segunda, cuatro por la tercera, ocho por la cuarta, y así sucesivamente hasta la casilla sesenta y cuatro». Sessa pedía, por tanto, que le recompensaran con el siguiente número de granos: 1 + 2 + 2 2 + 2 3 + 2 4 + … + 2 63 ; ¡más de 18 trillones!, que es la cosecha que se recogería al sembrar 65 veces toda la tierra. Por supuesto que el príncipe no pudo cumplir su promesa…
2. La geometría (medición de tierra) se inició, como ciencia, en el antiguo Egipto y en Babilonia por la necesidad de realizar mediciones terrestres.
3. El teorema de Pitágoras ha merecido la atención de muchos matemáticos, especialmente de la antigüedad. Actualmente están registradas unas 370 demostraciones de este teorema.
4. Se ha insinuado con bastante frecuencia que el teorema de Pitágoras no es deducción del gran matemático y fundador de la escuela del mismo nombre. La opinión más generalizada es que un miembro de su escuela formuló por primera vez el teorema en una época muy posterior. Pero por el mismo tiempo que vivió Pitágoras, es decir en el siglo VI a. de C., un matemático chino de nombre desconocido debió de haber llegado a la misma conclusión. En el Chon Pei Suan 0 Ching , libro matemático-filosófico, se encuentra una descripción que presenta dibujado, sin ningún género de dudas, un triángulo pitagórico con sus correspondientes relaciones.
5. Platón , en su escuela (la Academia), donde se discutían los más difíciles problemas de la lógica, de la política, del arte, de la vida y de la muerte, había hecho escribir encima de la puerta: «No entre el que no sea geómetra».
6. Arquímedes , pariente y amigo del rey Herón de Siracusa, le escribió una vez que con cualquier fuerza dada es posible mover cualquier peso dado (si hubiera otro mundo al que pudiera ir, podría mover el nuestro). Herón se asombró y suplicó que hiciera lo posible para llevar a cabo su proposición, y que le enseñara algún gran peso movido por una fuerza pequeña. Arquímedes pidió que un barco de tres mástiles de la flota real fuera remolcado a la playa con grandes esfuerzos de muchos hombre y, después de subir a bordo muchos pasajeros y la carga acostumbrada, se sentó a cierta distancia de la nave y, sin mucho esfuerzo, pero lentamente, puso en movimiento un sistema compuesto de poleas con sus manos, tiró de la nave uniformemente hacia él como si estuviera deslizándose por el agua. Plutarco. Life o Marcellus
7. En la primera mitad del siglo III, Diofanto de Alejandría usa los símbolos algebraicos y enuncia las reglas para resolver ecuaciones de primer y segundo grado.
8. Mohammeid ibn-Musa Al-Jwarizmi (780-846), matemático árabe, trabajó en la biblioteca del califa Al-Mahmun en Bagdag. De su nombre deriva la palabra algoritmo. Es el autor del trabajo Al-jabr wa´l muqäbala , del cual procede la palabra álgebra. Introdujo en occidente el sistema hindú de numeración decimal, que explicó con todo detalle en su obra Aritmética .
9. El matemático italiano Leonardo de Pisa (1170 - 1240) se le conocía más por Fibonachi o “hijo de Bonaccio”, un conocido mercader de Pisa que tenía negocios en el norte de África. En 1202 publicó un libro titulado Liber abaci , en el que incluye métodos y problemas algebraicos. La sucesión de Fibonacci aparece constantemente en la naturaleza. Citemos dos ejemplos concretos:
10. Si cuentas las escamas de una piña, observarás sorprendido que aparecen en espiral alrededor del vértice en número igual a los términos de la sucesión de Fibonacci
11. Lo mismo ocurre con las piñas de girasol; forman una red de espirales, unas van en sentido de las agujas del reloj y otras en el contrario, pero siempre las cantidades de unas y de otras son los términos consecutivos de la sucesión de Fibonacci.
12. Aritmética , de Johann Widman , publicado en Pforaheim en 1500, es el primer compendio práctico para comerciantes utilizado en Alemania.
13. François Viète (1540 - 1603) fue el primero en emplear letras para simbolizar las incógnitas y constantes en las ecuaciones algebraicas
14. El símbolo de raíz se empezó a usar en 1525 y apareció por primera vez en un libro alemán de álgebra. Antes, para indicar la raíz de un número se escribía “raíz de …”. Luego, para abreviar, se empezó a poner “r”. Pero si el número era largo, el trazo horizontal de la “r” se alargaba hasta abarcar todas las cifras. Así nació el símbolo de la raíz, como una “r” mal hecha
15. Las dos rayas = que indican igualdad las empezó a utilizar un matemático inglés llamado Robert Recorde que vivió hace más de cuatrocientos años. En uno de sus libros cuenta que eligió ese signo porque “dos cosas no pueden ser más iguales que dos rectas paralelas”
16. A finales del siglo XVI, un gran matemático francés, François Viète , descifraba con toda facilidad los mensajes secretos de los ejércitos españoles de Felipe II (que serían bastante ingenuos, dado lo que había). Los españoles no lo dudaron ni un instante y acusaron a Viète, ante el Papa, de estar aliado con el diablo.
17. La definición de logaritmo fue dada por John Neper (1550 - 1617) geométricamente como razón entre dos magnitudes.
18. La primera vez que aparece en la historia la idea de lo que iba a ser más tarde la derivada de una función en un punto es con Fermat , hacia 1625. Sin embargo, Fermat no disponía aún de la idea de límite, y así lo único que podía hacer en el cociente incremental ?y / ?x era directamente ?x = 0, lo cual es incorrecto, claro. Aún así, Fermat aplicó la idea al cálculo de máximos y mínimos y de tangentes a curvas.
19. La teoría de probabilidad tiene su origen en los juegos de azar. Hacia 1650, en Francia, un jugador llamado De Mére consultó al matemático Blaise Pascal algunas cuestiones relacionadas con el juego de dados. Pascal mantuvo correspondencia con Fermat, Huygens y Bernoulli. Gracias a todos ellos, la teoría de la probabilidad pasó de ser una mera colección de problemas aislados, relativos a algunos juegos, a ser un sector importante de las matemáticas.
20. Los signos de multiplicación x y división : fueron introducidos por William Oughtred (1574 - 1660) en el año 1657
21. En 1659, en el Álgebra alemana , de Jhoan Rahn , aparece el signo ÷ para indicar la división
22. En su Invention Nouvelle en Algebre , el francés Albert Girard (1595 - 1632) introduce por primera vez el uso de los paréntesis, explica el método de descomposición de un polinomio en factores, enuncia el teorema fundamental del álgebra, y usa el ___ colocado entre el numerador y el denominador para indicar una fracción algebraica o numérica
23. En 1662 el honorable Robert Boyle (1627 - 1691) , séptimo hijo del conde de Cork, llevó a cabo un estudio de los gases que culminó en el reconocimiento de una interdependencia sencilla entre la presión y el volumen. Ley de Boyle: P V = cte (a T y m ctes.)
24. Robert Boyle sostuvo la idea de que todo trabajo experimental debía ser publicado con claridad y rapidez, para que otras personas pudieran repetirlo, confirmarlo y aprender con ello.
25. A René Descartes se le considera como el creador de la Geometría Analítica. Una de sus mayores aportaciones fue el traducir el leguaje geométrico, casi experimental, al lenguaje algebraico.
26. John Théophile Desaguliers (1683 - 1744), físico inglés de origen francés, fue el primer autor que empleó la palabra conductor, para designar los cuerpos que permiten el paso de la corriente eléctrica, y aislante para referirse a los que oponen gran resistencia al paso de dicha corriente.
27. La palabra «derivada» será introducida por Lagrange a final del siglo XVIII, pero de nuevo está ausente la noción de límite.
28. La notación y’ y f´(x) , para la derivada, fueron introducidas por Lagrange , mientras que las formas dy/dx o df/dx se deben a Leibniz .
29. Leibniz fue el primero que utilizó el término función. Para él y para los matemáticos del siglo XVIII, el concepto de relación funcional en sentido matemático estaba más o menos identificado con el de una fórmula algebraica sencilla que expresara la naturaleza exacta de esta dependencia. Leibniz también introdujo los términos constante, variable y parámetros y la notación de derivada anteriormente citada.
30. Leonard Euler estudió la sucesión (1 + 1/n) n . Al límite de esta sucesión se le llamó número e , inicial de su apellido.
31. El primer matemático que utilizó los determinantes en sentido moderno fue el suizo Gabriel Cramer (1704-1752), el año 1750.
32. El análisis de Fourier fue inventado por Jean Baptiste Joseph, barón de Fourier, físico francés, en 1807. Demostró que una onda periódica cuya longitud sea ? se puede sintetizar con una suma de ondas armónicas cuyas longitudes son ?, ?/2, ?/4, etc.
33. El Barón Joseph Fourier (1768-1830) propuso la notación moderna para las integrales (v.)
34. “¡Eureka! num = ??+ ??+ ?”.
Esta enigmática inscripción es lo que escribió en su cuaderno de notas Carl Friedrich Gauss cuando descubrió que todo número entero positivo es la suma de tres números triangulares, que son los que cumplen la forma n (n+1) / 2.
35. Leonard Euler (1707-1783), matemático suizo, simbolizó en 1777 la raíz cuadrada de -1 con la letra i (inicial de imaginario).
36. La palabra cero deriva probablemente de “zephirum”, forma latinizada del árabe “sifr” que es, a su vez, una traducción de la palabra hindú “sunya” que significa vacío o nada.
37. La multiplicación era considerada muy difícil y, hasta el siglo XVI, solo se enseñaba en las universidades.
38. Hasta fines del siglo XVIII, los números negativos no fueron aceptados universalmente.
39. Los matemáticos de la India, en el siglo VII, usaban los números negativos para indicar deudas.
40. Gerolamo Cardano, en el siglo XVI, llamaba a los números negativos “falsos”, pero en su ” Ars Magna ” (1545) los estudió exhaustivamente.
41. John Wallis (1616 - 1703), en su “Arithmetica Infinitorum” (1655), “demuestra” la imposibilidad de su existencia diciendo que “esos entes tendrían que ser a la vez mayores que el infinito y menores que cero”.
42. Leonard Euler, es el primero en darles estatuto legal; en su Anleitung Zur Algebra (1770) trata de demostrar que (-1)(-1) = +1
43. El primero en usar la coma para separar la parte decimal de la fraccionaria fue el astrónomo italiano Giovanni Magini. La invención de los logaritmos generalizó el uso de los números decimales y el escocés John Napier, inventor de los logaritmos neperianos, recomendó en 1617 el uso del punto; el caos siguió durante todo el siglo XVIII aunque al final solo quedaron en competencia el punto y la coma. En el continente europeo el asunto se resolvió en 1698, cuando Leibnitz, propuso usar el punto como símbolo de multiplicación (”en lugar del signo x, que se confunde con x, la incógnita”); quedó así la coma para separar la parte decimal del número. En Inglaterra, sin embargo, donde se habían cerrado las puertas al alemán Leibnitz, se siguió utilizando el símbolo x para la multiplicación y el punto para separar los decimales. En España y América también se usó, y se sigue aceptando, la coma elevada.
44. Los griegos desarrollaron las secciones cónicas unos 400 años antes de nuestra era; unos 2000 años después, Kepler demostró que las trayectorias de los planetas son elipses y Galileo descubrió que las trayectorias de los proyectiles son parábolas.
45. El hecho de que tengamos diez dedos en las manos y diez dedos en los pies, ha determinado la adopción del sistema decimal de numeración; aunque con el correr de los siglos se han propuesto y utilizado otros sistemas.
46. El sistema sexagesimal (base 60) fue creado por los babilonios hacia el año 200 antes de Cristo y se usa todavía para medir el tiempo y los ángulos.
47. La civilización maya floreció en Mesoamérica alrededor del siglo IV de nuestra era. Se sabe que tenían dos sistemas de numeración, los dos en base 20. Los aztecas también usaban un sistema vigesimal.
48. En el siglo XVIII, el naturalista francés Georges L. Buffon propuso un sistema de base 12.
49. Joseph L. Lagrange, matemático francés del siglo XVIII, propuso un sistema con once símbolos (base 11).
50. Gottfried W. Leibnitz, inventó el sistema binario (base 2) usado hoy en los ordenadores. Leibnitz vio en este sistema la imagen de la Creación; se imaginó que la unidad (1) representaba a Dios y el cero (0) la nada, e inventó un sistema filosófico basado en esas premisas.
En la torre Eiffel esta grabado el nombre del ilustre científico francés Fourier…
ejemplos de series de fourier periódicas.
Funciones Pares e Impares
Es importante analizar una función respecto a su simetría porque dependiendo de su paridad su expansión de fourier puede simplificarse considerablemente.
* Si f(t) es par, entonces f(t) = f(-t), y la gráfica es simérica respecto al eje vertical. (El eje vertical hace de espejo).
Y POR LO TANTO el coeficiente bn = 0
* Si f(t) es impar, entonces f(t) = -f(-t), y la gráfica es simérica respecto al origen. (La gráfica del cuadrante I es la misma que la del cuadanteIII).
Y POR LO TANTO el coeficiente an = 0 y a0 = 0.
Propiedades de Utilidad:
- La suma de funciones impares es una función impar.
- El producto de dos funciones pares es una función par.
- El producto de dos funciones impares es una función par.
- La derivada de una función par es una función impar.
- La derivada de una función par es una función impar.
Series de Fourier
Introducción
En 1807 Jean Baptiste Joseph Fourier, ingeniero y matemático francés, postuló que:
-Una función arbitraria f(t) de periodo
puede ser representada por una serie trigonoétrica de sumas de senos y cosenos de la forma:
-Una función arbitraria f(t) de periodo
puede ser representada por una serie trigonoétrica de sumas de senos y cosenos de la forma:
que se puede escribir como:
y resolviendo los coeficientes de Fourier se tiene las fórmulas de Euler:
-Fué Fourier quien desarrolló esta fórmula de una manera útil y aplicable, a pesar de que Bernoulli, D'Alember y Euler por 1750 usaron ya esta idea.

D'Alember(1717-1783)
Euler(1707-1783)
-Fué tal el impacto y la sorpresa de esta serie sobre la comunidad científica de ese entonces que Laplace, Poisson y Lagrange se oponieron duramente a Fourier, lo que causó el retraso de la publicación del trabajo de Fourier Théorie Analytique de la Chaleur.
Poisson(1781-1840)
Laplace(1749-1827)
Lagrange(1736-1813)
2009-11-08
complejos
El número
complejo
Historia.-
El gran matemático Diofanto (275 d.C) construyó un triángulo con una cuerda en la que había realizado 12 nudos (equidistantes). Los lados medían 3, 4 y 5 unidades
Evidentemente el triángulo es rectángulo, cumple el teorema de Pitágoras:
32 + 42 = 52
Al ser un triángulo rectángulo es fácil comprobar que el área es 6 unidades.
Con la misma cuerda trató de construir otro triángulo rectángulo de forma que su área fuese 7 unidades.
Su planteamiento fue el siguiente
un cateto mediría x
como el área debía ser 7, el otro cateto será 14/x.
la hipotenusa debe cumplir el teorema de Pitágoras
pero por otra parte la suma de sus lados debe ser 12
Por tanto se debe cumplir la ecuación:
De donde se llega fácilmente a:
Cuya solución Diofanto expresó como
Pero no conocía ningún número que elevado al cuadrado fuese igual a –1, por tanto, el problema no tenía solución.
Este problema planteado por Diofanto tardaría siglos en resolverse.
En 1777 el matemático suizo Leonhard Euler (1707 - 1783) simbolizó la raíz cuadrada de –1 con la letra i (por imaginario).
Euler
Definición.- El término número complejo describe la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra i).
La propiedad más importante que caracteriza a los números complejos es el teorema fundamental del álgebra, que afirma que cualquier ecuación algebraica de grado n tiene exactamente n soluciones complejas.
Los números complejos son una extensión de los números reales, cumpliéndose que  . Los números complejos representan todas las raíces de los polinomios, a diferencia de los reales
. Los números complejos representan todas las raíces de los polinomios, a diferencia de los reales
Representación binomial
Un número complejo se representa en forma binomial como:
La parte real del número complejo y la parte imaginaria, se pueden expresar de varias maneras, como se muestra a continuación:
Si el complejo está escrito en forma exponencial z = r eiφ, entonces |z| = r. Se puede expresar en forma polar como z = r (cosφ + isenφ), donde cosφ + isenφ = eiφ es la conocida fórmula de Euler.
Conjugado de un número complejo
El conjugado de un complejo z (denotado como  ó
ó  ) es un nuevo número complejo, definido así:
) es un nuevo número complejo, definido así:
Representación trigonométrica (polar) y representación geométrica
Representamos el número complejo z en el plano de números complejos como un punto con coordenadas (a, b), denominado vector de posición.
Trazamos la distancia desde el punto (0,0) hasta (a, b), a la que llamaremos r, y, que como se ha visto antes, es igual al módulo de z, expresado | z | .
Esta distancia forma, con respecto al eje real positivo, un ángulo, denominado  .
.
OPERACIONES CON COMPLEJOS
Adición de números complejos
La suma de dos números complejos es otro complejo que tiene por componente real la suma de las componentes reales y por componente imaginaria la suma de las componentes imaginarias de los sumandos.
El producto de dos números complejos es otro complejo que se obtiene escribiendo los complejos dados en forma binómica y realizando la multiplicación algebraica, teniendo en cuenta que i2 = -1
Es decir:
Variables y funciones Complejas
Un símbolo, tal como z, que representa a cualquier elemento de un conjunto de números complejos se llama variable compleja.
Si a cada valor que puede tomar la variable compleja z le corresponde uno o más valores de una variable compleja w, decimos que w es una función de z y escribimos w = f(z). La variable z frecuentemente es llamada variable independiente, mientras que la variable w es la variable dependiente. El valor de una función en z = a se representa f (a).
Funciones exponenciales
Funciones exponenciales son las definidas por
donde ln a es el logaritmo natural de a.
Funciones trigonométricas
Muchas de las propiedades de las funciones trigonométricas reales son también válidas para el caso de las funciones trigonométricas complejas. Por ejemplo:
Funciones logarítmicas
Si z = ew, entonces escribimos w = ln z, llamado el logaritmo natural de z. Entonces la función logaritmo natural es la inversa de la función exponencial y podemos definirla por
Esa función es multivaluada, por ello se define el valor principal o rama principal de la función ln z como ln z +iq, donde . Esta definición es un convenio, se podría definir de igual forma tomando q en cualquier intervalo de amplitud 2p .
La fórmula de De Moivre
nombrada así por Abraham de Moivre afirma que para cualquier número complejo (y en particular, para cualquier número real) x y para cualquier entero n se verifica que:
LOS NUMEORS COMPLEJOS ESTÁN DESORDENADOS
Por las propiedades de la relación de orden sabemos que si multiplicamos a ambos lados por i la desigualdad cambia de sentido (al ser i en este caso un número negativo). Usando que i2 = -1 y que i·0 = 0 queda:
Lo cual es imposible.
-Supongamos ahora que 0 es menor o igual que i:
Como ahora i es positivo si multiplicamos a ambos lados por él la desigualdad se debe mantener igual. Usando las mismas propiedades anteriores obtenemos:
Que como antes es absurdo.
Por tanto, como acabamos de ver, no podemos definir una relación de orden en el cuerpo de los números complejos cuya restricción a los números reales sea la que conocemos de toda la vida
Suscribirse a:
Comentarios (Atom)